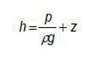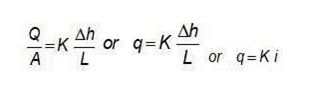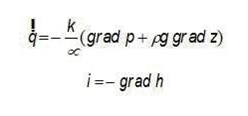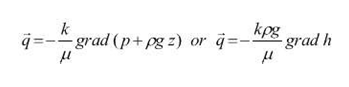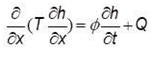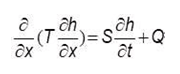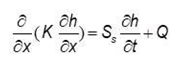¿Cómo fluye el agua a lo largo de un medio poroso? Te lo explicamos en detalle en este extracto de texto, extraído de uno de los módulos del “Curso de Hidrogeología aplicada a minería”
- Flujo de agua en medios porosos
El flujo de agua que bien es utilizado para el abastecimiento de una mina, o que se intercepta por una mina, forma parte de un ciclo natural que se origina en la precipitación de agua de lluvia, escorrentía y/o infiltración en el terreno, descarga en masas de agua superficial (ríos, lagos) y en el mar. Durante este transcurso, el agua se evapora y vuelve a precipitar, cerrando el ciclo.
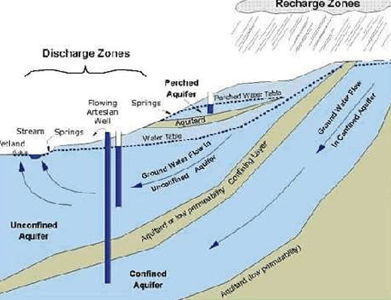
Durante su infiltración, el agua se mueve en el medio geológico donde las interacciones pueden ser diver- sas y donde fundamentalmente adquirirá su composición química, que podrá ser variable a lo largo de su trans- curso por el medio. La Figura 1 1 muestra esquemáticamente la circulación del agua en el medio subterráneo y se indican algunos de los conceptos que se explican con más detalle en las siguientes secciones.
Una vez en el terreno, el agua empapa el material geológico y desciende por efecto de la gravedad desde cotas más altas a cotas más bajas. El agua se mueve por donde tiene menos dificultad (materiales más permea- bles) y los materiales menos permeables ofrecen más resistencia a su paso. Los materiales geológicos que están saturados y que pueden transmitir el agua con facilidad, se denominan acuíferos, mientras que los que no la transmiten se llaman acuífugos. Los que la transmiten con dificultad se denominan acuitardos.
Igualmente, el agua se mueve en el suelo, que es la zona que en condiciones habituales se desarrolla desde la superficie del terreno hasta la profundidad radicular de las plantas. El suelo, a diferencia de los acuíferos, no suele estar empapado en agua, y decimos que está parcialmente saturado. Por debajo de la zona radicular de las plantas (o de lo que llamamos “suelo”) puede existir un espesor de material geológico sin saturar que se denomina comúnmente “zona no saturada” donde ocurren gran parte de los procesos de transferencia de agua hacia los acuíferos. El agua se mueve a través de él hasta ocupar totalmente el espacio vacío del material geológico: en este momento se conforma el acuífero.
La Figura 1 2 ilustra esta descripción. De arriba abajo se muestra un tramo de gravas “seco”, que sería par- te de la zona no saturada; inmediatamente por debajo se encuentra una zona llamada “capilar” que definiremos más adelante y el acuífero, o zona completamente saturada que transmite agua -de hecho se observa bien el rezume de agua-. En la base de las gravas que están saturadas y transmiten el agua se encuentran unas areniscas que, si bien están saturadas en agua, deben ser mucho menos permeables y conforman la “base del acuífero”.
El contacto entre la zona capilar y el acuífero es lo que conocemos como nivel freático.

Una vez descritos algunos de los conceptos, veamos su descripción cuantitativa.
- Porosidad:
La porosidad es el volumen de espacio vacío dividido por el volumen total de roca. Es un parámetro adimensional:
ϕ = (Vol.vacío)/(Volumen roca)
- Índice de poros:
Es la relación que hay entre el volumen vacío y el volumen sólido de la roca:
e = (Vol.vacío)/(Volumen sólido)
, por extensión, ambos parámetros se relacionan de la siguiente manera:
ϕ = e/e+1
y
e = ϕ/ ϕ-1
Si pensamos en el agua subterránea como un fluido que circula a través de un acuífero y que este acuífero puede ser dividido en secciones, entonces tenemos en concepto de:
- Porosidad superficial:
Es el espacio vacío en una determinada sección de material poroso.
- Área superficial específica:
Es la relación entre el área superficial del vacío y el volumen total de roca. Tiene unidades de (L-1) y es un parámetro que da cuenta del área potencialmente reactiva que tiene un determinado acuífero
Ssp = (Área superficial total del conjunto de vacíos)/(Volumen total de medio)
típicamente tiene los siguientes valores:
– arena ≈ 1.5·104 m2/m3
– arena fina ≈ 1.5·105 m2/m3
– arcilla ≈ 1.5·109 m2/m3
– agua “adherida”
Es agua adherida a la superficie de los granos a través de la influencia de las fuerzas y atracción molecular, no puede desplazarse por gravedad o por gradiente de presión, pero puede ser importante para la composición del agua y durante procesos de intercambio iónico.
– Agua “libre”
Es agua que queda fuera del campo de atracción, puede desplazarse por el medio.
– Porosidad “cinemática” o “eficaz”
Es un concepto ligado al espacio por el que circula esta agua, más que al concepto de volumen
ϕc = (volumen de agua que se desplaza)/(volumen total de roca)
2. Desplazamiento del agua en el acuífero
Al principio hemos indicado que el agua se mueve por efectos de gravedad desde zona de mayor elevación a zonas de menor elevación. Formalmente esto es debido a las diferencias de energía del agua ubicada en dos puntos del acuífero. La energía del agua en un punto del acuífero se describe como:
El primer término está formado por la velocidad del agua (v) y la aceleración de la gravedad (g) y es el término cinético; el segundo, de presión, incorpora la presión del agua (p), su densidad (ρ) y la gravedad; el tercero el potencial, es la elevación con respecto a una cota de referencia (z).
En acuíferos la velocidad del agua es muy lenta y por tanto, el término cinemático muy pequeño frente a los otros y por este motivo se desprecia. Solamente hablamos de potencial hidráulico o nivel piezométrico:
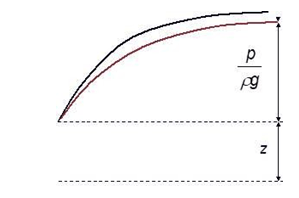
En una sección hipotética, se descompone de la siguiente manera:
Donde la línea superior, en negro sería la superficie del terreno y la inferior, en rojo, el nivel freático. Nó- tese que el nivel freático, por definición, es la superficie donde la presión de agua es nula. En la práctica esta magnitud es lo que uno mide en un sondeo al introducir la sonda de nivel:
En un sondeo se mide la profundidad a la que se encuentra el nivel de agua con respecto a una cota de referencia. Si el flujo se puede asumir como horizontal con respecto al sondeo, entonces se puede decir que el potencial hidráulico que medimos en B es el mismo que corresponde a A.
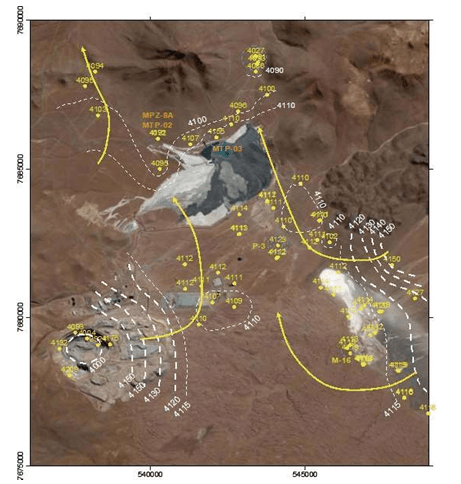
Si tenemos suficientes medidas de nivel repartidas en un dominio de estudio y estas medidas se toman por un tiempo suficientemente largo podemos tener mapas piezométricos y evoluciones del nivel con respecto al tiempo. Los primeros nos indican la distribución (y dirección) del flujo de agua en el espacio 2D horizontal, mientras que la evolución en el tiempo refleja la situación del acuífero entre dos situaciones determinadas. En la Figura 1.3 se muestra un mapa piezométrico de una zona minera y en la Figura 1 4 se muestra la evolución del nivel en un pozo a lo largo del tiempo.

2.2. Tipos de acuíferos en función del nivel piezométrico
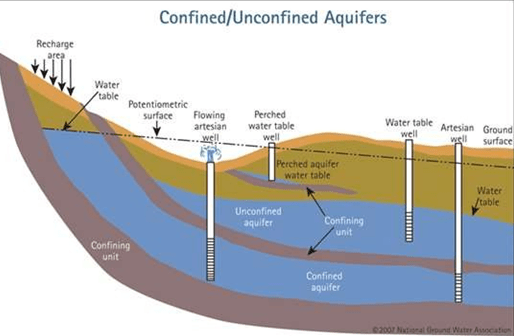
Un determinado pozo, en función de la posición del nivel piezométrico que esté midiendo y de las for- maciones permeables y menos permeables, de pueden clasificar como confinados, no confinados (libres) y confinados surgentes. En la Figura 1 5 se muestra esta tipología. Cuando el nivel freático está en contacto con la atmósfera, hablamos de acuífero libre; cuando el nivel está por encima del techo del acuífero, hablamos de acuífero confinado. Los pozos pueden ser ranurados en acuíferos libres o en acuíferos confinados (llamados también pozos artesianos). Si el nivel piezométrico está por encima del nivel del terreno, entonces el pozo es surgente. Puede haber zonas saturadas del terreno que no estén conectadas al sistema de flujo general, y enton- ces hablamos de acuíferos “colgados”.
2.3. Ley de Darcy
Henry Darcy estableció empíricamente que el flujo de agua a través de una formación puede calcularse como: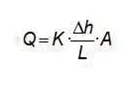
donde:
Q = caudal de agua A = área de paso
∆h/L = diferencia entre en nivel piezométrico a ambos lados de la formación (gradiente hidráulico, i) K = constante que depende de la formación rocosa
Si dividimos a ambos lados de la ecuación por el área de paso, se obtiene:
donde q es el flujo de agua (caudal por unidad de superficie perpendicular al flujo) y no la velocidad a la que se desplaza el agua, a pesar de tener las mismas magnitudes y expresarse en las mismas unidades. Para obtener la velocidad real del agua se debe dividir el flujo por la porosidad cinemática.
v = q/ϕ
Este parámetro se usa frecuentemente en estudios ambientales para saber la llegada de un frente de conta- minante, o en estudios de modelización química para calcular las interacciones que tiene el agua con el medio.
En realidad, K varía con la viscosidad del agua y si expandimos i, se obtiene:
, donde k es la “permeabilidad intrínseca”. Es una propiedad que depende de la roca, independiente del fluido y del contenido del fluido.
Se puede escribir de la siguiente forma para obtener el darcy: “la permeabilidad del medio donde el flujo de 1cm3/s se obtiene a través de una sección de 1cm2 para un fluido de viscosidad de 1cP y con un gradiente de presión de 1 atm/cm”:
(L2) 1 darcy = 0.987 ·10-12 m2
Si expandimos la ley de Darcy para un fluido incompresible:
. definimos:
, como “conductividad hidráulica”, K, con dimensiones de velocidad (LT-1) (en realidad no lo es). Para problemas no-isotérmicos, varía hasta un 20% entre 10ºC y 30ºC).
2.4. Concepto de transmisividad (T) y de espesor saturado (b)
Se define como espesor saturado (b) el grosor de un acuífero con la porosidad completamente “llena” de agua. Para un acuífero confinado, está limitado por la base y el techo del acuífero. En un acuífero libre o no confinado, por el nivel freático y la base.
Definimos transmisividad como el producto de la conductividad hidráulica por el espesor saturado. Es la magnitud que indica la capacidad de un acuífero a transmitir agua (o a permitir que el agua fluya a través del medio que lo configura), o el agua que puede pasar por una sección vertical de acuífero, por unidad de anchura.
T = K·b
Así, la transmisividad tiene dimensiones de L2·T-1
2.5. Concepto de almacenamiento (S)
Es la cantidad de agua liberada por la unidad de superficie de un acuífero por unidad de descenso en el nivel piezométrico (Figura 1.6). Si el acuífero es libre (conectado a la atmósfera) coincide con la porosidad “drenable” o Specific yeld (Sy). Si el acuífero es confinado, se relaciona con la compresibilidad del sólido y del agua.

2.6. Ecuación general de flujo
A efectos de completitud del capítulo, puede decirse que si combinamos la ley de Darcy con la de conser- vación de la masa, entonces tenemos la ecuación general de flujo (en 1-D):
, o bien:
, o lo que es lo mismo: