
Técnicas de perforación más comunes
Fragmento de uno de los módulos del “Curso de diseño y ejecución de micropilotes“. Técnicas de perforación más comunes (micropilotes) En este apartado revisaremos algunas de las metodologías más empleadas para realizar perforaciones destinadas a la ejecución de micropilotes, describiendo tanto equipos como útiles de corte, sistemas de barrido (limpieza

Voladuras amortiguadas
Fragmento de uno de los módulos del “Curso de diseño de voladuras“. VOLADURAS AMORTIGUADAS (Buffer blasting) Las voladuras amortiguadas son aquellas en las que el diseño de la última o dos últimas filas ha sido modificado tanto geométricamente, reduciendo piedra y espaciamiento, cono en cantidad de energía mediante reducción de

Métodos de mejora ante problemas de licuefacción
Fragmento de uno de los módulos del “Curso de licuefacción de suelos durante terremotos: fundamentos y técnicas de mitigación“. Métodos de mejora ante problemas de licuefacción. Uno de los métodos: Contenido1.1. Desaturación. Tratamientos biotecnológicos1.1.1. Desaturación parcial inducida1.1.2. Tratamientos biotecnológicos 1.1. Desaturación. Tratamientos biotecnológicos En los últimos años se han

Análisis del entorno psicoambiental: disponibilidad de materiales, maquinaria y mano de obra especializada
Fragmento de uno de los módulos del “Curso de Experto en diseño geotécnico de cimentaciones superficiales“. Hoy en día, es bien conocido que la especialización singular en cualquiera de las ramas de la ingeniería civil dejando de lado otras disciplinas suele estar abocado al fracaso: la visión multidisciplinar de cualquier

¿Cómo diseñar y modelizar una planta para el tratamiento de minerales y la recuperación de sustancias valiosas de los residuos sólidos urbanos e industriales?
El campo de las técnicas de tratamiento y concentración de minerales abarca también la recuperación de sustancias valiosas contenidas en residuos industriales, tales como escorias, chatarras, etc., e incluso trata de recuperar dichas sustancias
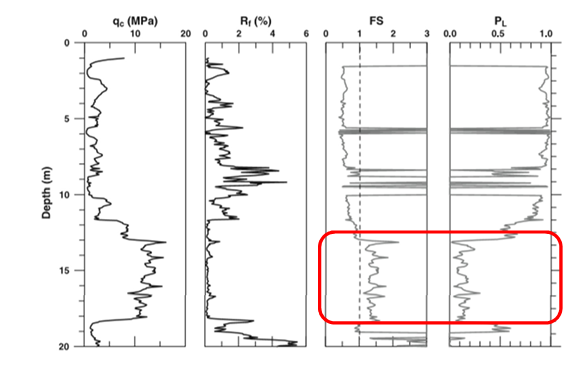
Índice de riesgo por licuefacción
A la vista de la incertidumbre del índice LPI en el caso de utilizar el CPT como herramienta de caracterización de la licuefacción potencial, Lee et al. (2003) propusieron un índice alternativo, denominado Índice de Riesgo por Licuefacción (Liquefaction Risk Index, IR) basado en los resultados de campañas mediante equipos

Auscultación de presas
CONTROL HIDRÁULICO. Dado que la presa es un elemento que tiene por función contener el agua de un cauce natural, el control de la presión del agua es una actividad crítica. Una cierta cantidad de agua se filtra a través de, debajo y alrededor todas las presas. El agua se
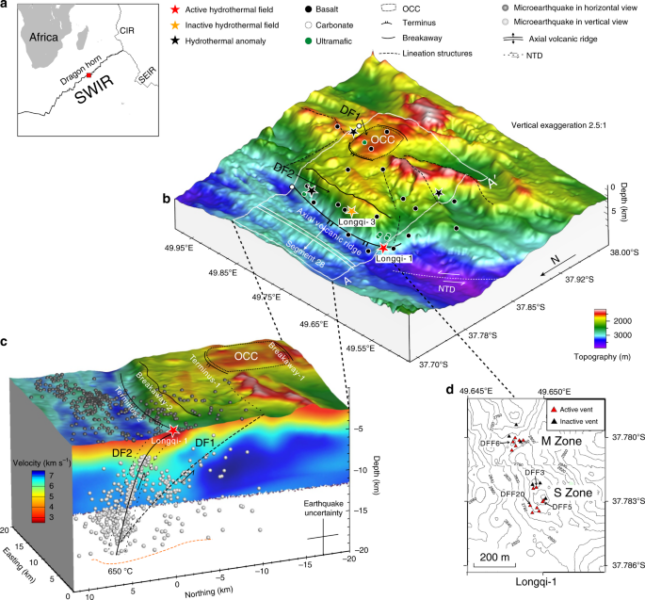
Procesos que controlan la composición de las aguas marinas
Si recordamos, de nuestros estudios de educación primaria, podemos darnos cuenta de lo fundamental que es el tema de la geoquímica de aguas continentales. En números, sólo el 4% del agua del planeta es agua dulce, de la que depende nuestra supervivencia. También sabemos cómo de importante es este recurso

¿Qué es la metodología BIM y qué beneficios aporta?
Artículo escrito por David Simón, docente de varios cursos dentro de la metodología BIM de nuestro centro. Las referencias a los términos BIM o “modelado de información de construcción” (Building Information Modeling) están, en estos momentos, a la orden del día. Si buscamos los términos en Internet, producirán varios millones

Efectos de la degradación de los ecosistemas en los sectores económicos
La degradación de los ecosistemas tiene un efecto directo sobre la pérdida del Capital Natural y los servicios ecosistémicos. En este artículo extraído del “Curso de Restauración ecológica de espacios mineros” te explicamos exactamente cuáles son las consecuencias en las actividades industriales.

Historia de la dinosauriología
Las bases actuales de la Paleontología, sus conceptos, métodos y cuerpo de conocimientos, proceden de comienzos del siglo XIX, pero ¿conoces la historia de la una de las más destacadas ramas dentro de ella? En este extracto del “Curso de Paleontología de dinosaurios” podrás descubrir cómo se fue desarrollando la

¿Qué son los Sistemas de Información Geográfica (SIG) y cómo funcionan?
Los Sistemas de Información Geográfica son herramientas de análisis que ofrecen la posibilidad de identificar las relaciones espaciales de los fenómenos que se estudian. En este artículo extraído del módulo I del “Curso de SIG aplicado al Medio Ambiente” te explicamos la diferencia con otros paquetes de software gráficos, cuáles
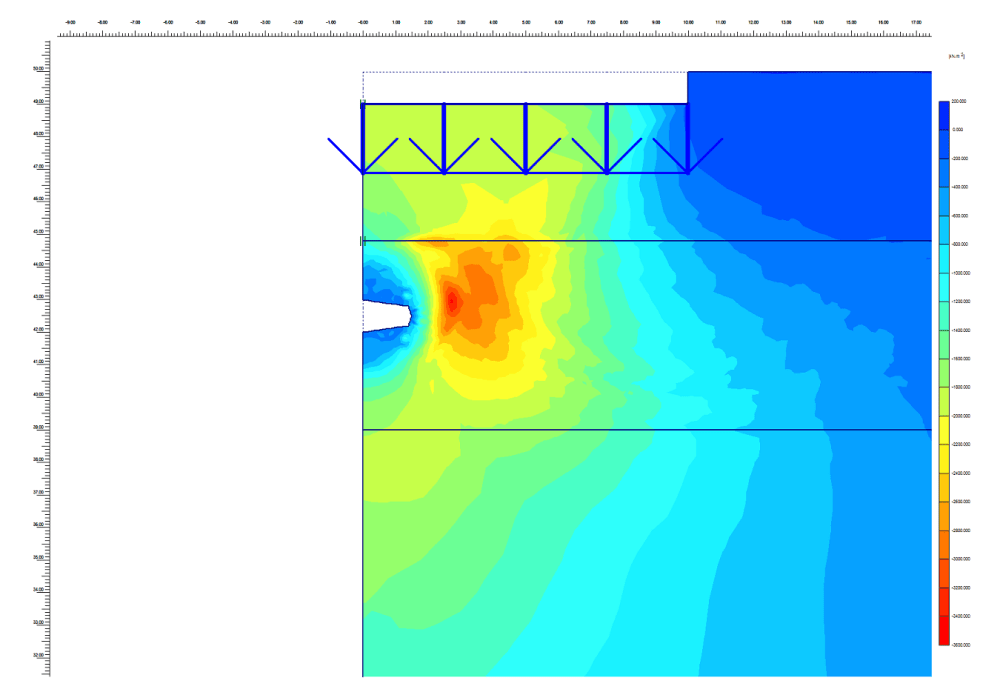
Fundamento y origen del Método de los Elementos Finitos (MEF)
¿Conocéis el Método de los Elementos Finitos?, ¿sabéis para qué se utiliza?, ¿sabéis cómo y cuándo se fundó el programa Plaxis 2D? Descubrid todo esto y mucho más en este extracto del módulo I del curso online “Modelización numérica con Plaxis 2D”

Qué tipos de mampostería se emplean en la construcción
La mampostería es un sistema de construcción más común de lo que se cree. A pesar de su aspecto rudimentario y tosco, es esencialmente útil en algunas edificaciones para garantizar resistencia y durabilidad.

Conocimiento previo del área a cartografiar
Pasos antes de ir al terreno ¿Conocéis todos los pasos que debéis tomar antes de ir a un terreno?, ¿sabéis todos los conocimientos previos que necesitáis antes de cartografiar?, ¿cuáles son los mejores organismos para buscar información cartográfica? Os respondemos todo esto y mucho más en este extracto del módulo
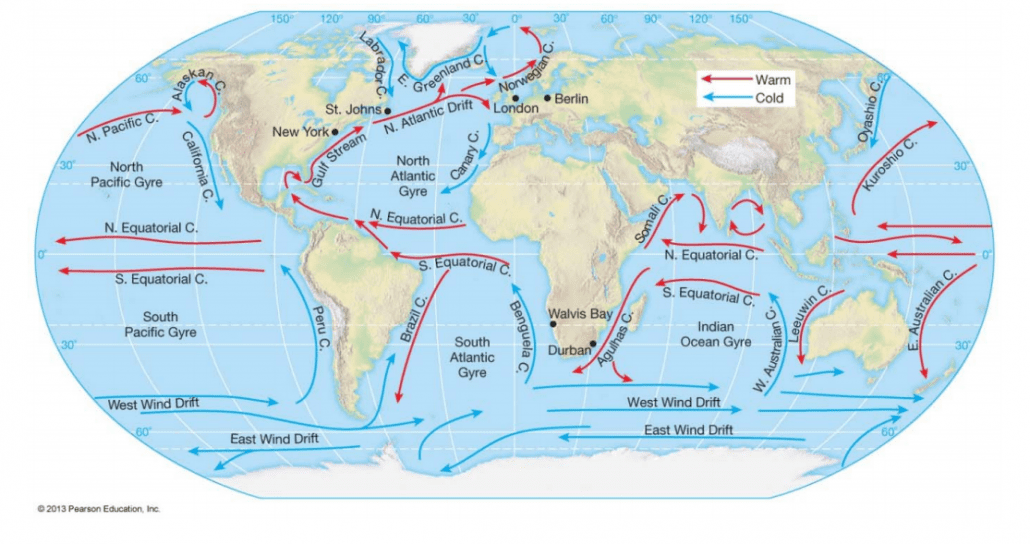
El recurso energético marino
¿Sabéis cuáles son los principales recursos energéticos marinos? ¿Qué son las mareas y por qué suceden?, ¿cuáles son los tipos de olas?, todas estas respuestas y muchas más en este extracto del módulo II del “Curso de energías marinas”.

Restauración ecológica de la teoría a la práctica
¿Qué es la memoria de los ecosistemas?, ¿cuál es la dinámica de los ecosistemas naturales y degradados?, ¿por qué sucede la degradación de un ecosistema?, os respondemos todas estas interrogantes y muchas más en este extracto del módulo II del curso “Restauración ecológica de ecosistemas forestales”.
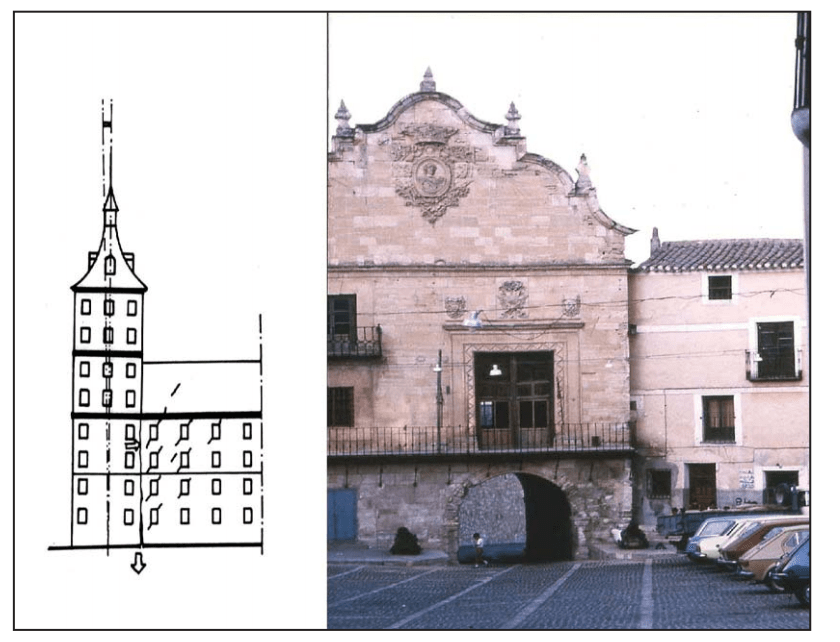
Los procesos patológicos y su diagnóstico
¿Sabéis las clases de movimientos originados por un proceso patológico en la cimentación de una edificación? Os explicamos cada uno en este extracto del módulo III del “Curso de patología e intervención en cimentaciones de edificación“.

¿Qué es un glaciar?, ¿cuáles son las definiciones más importantes de este tema?
¿Conocéis cómo se forman los glaciares? ¿Habéis leído sobre las definiciones más importantes en glaciología? Os explicamos todo sobre este interesante tema en este extracto del “Curso básico de glaciología”
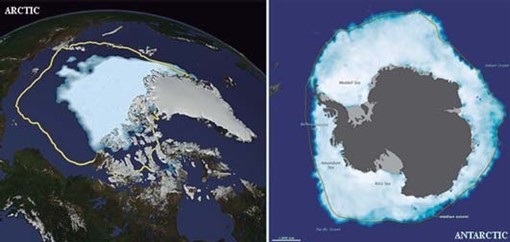
Transformación y degradación de los ecosistemas
Tras este breve paseo por el Antropoceno, es evidente que el crecimiento acelerado de la población humana y el aumento en la demanda de los recursos naturales han generado una transformación y alteración de los ecosistemas. Este conjunto de procesos es lo que se conoce como cambio global: cambios en

Notas sobre el calentamiento global y las energías renovables
¿En qué consiste el envejecimiento y desmantelamiento de la flota nuclear? ¿Cúales son las políticas en materia de energías renovables de la Union Europea? Te explicamos esto y mucho más en este fragmento de texto, extraído de uno de los módulos

La importancia del terreno en los proyectos de construcción
Todos los proyectos constructivos, en mayor o menor medida, tienen que buscar apoyarse en el terreno para conseguir equilibrio, estabilidad y funcionalidad de sus estructuras.

Clasificaciones de imágenes de satélite
¿Cómo se clasifican las imágenes obtenidas por satélite? Te lo explicamos en detalle en este extracto de texto, extraído de uno de los módulos

Flujo de agua en medios porosos
¿Cómo fluye el agua a lo largo de un medio poroso? Te lo explicamos en detalle en este extracto de texto, extraído de uno de los módulos

